Embark on an academic exploration of AP Calculus AB First Semester Review, a comprehensive guide designed to equip you with a solid foundation in the essential concepts of calculus. This review encompasses functions and their graphs, limits and continuity, derivatives, applications of derivatives, integrals, and applications of integrals, empowering you with a thorough understanding of this fundamental branch of mathematics.

As we delve into the intricacies of calculus, we will unravel the mysteries of functions and their graphical representations, exploring their domains, ranges, asymptotes, and intercepts. We will then venture into the realm of limits and continuity, grasping their significance and mastering various techniques for evaluating limits.

Our journey continues with the concept of derivatives, where we will uncover their geometrical interpretation and delve into the power rule, product rule, quotient rule, and chain rule for finding derivatives. Armed with this knowledge, we will explore the practical applications of derivatives in solving optimization problems, related rates problems, and curve sketching.

Functions and their Graphs: Ap Calculus Ab First Semester Review

Functions are mathematical relations that assign a unique output to each input. The graph of a function is a visual representation of the relationship between the input and output values.

The key concepts of functions and their graphs include:

• Domain:The set of all possible input values.
• Range:The set of all possible output values.
• Asymptotes:Lines that the graph approaches but never touches.
• Intercepts:The points where the graph crosses the x-axis or y-axis.

There are many different types of functions, each with its own unique graph. Some common types of functions include:

• Linear functions:Graphs of linear functions are straight lines.
• Quadratic functions:Graphs of quadratic functions are parabolas.
• Exponential functions:Graphs of exponential functions are curves that increase or decrease rapidly.
• Logarithmic functions:Graphs of logarithmic functions are curves that are the inverse of exponential functions.

There are a variety of techniques that can be used to graph functions. Some common techniques include:

• Using intercepts:The intercepts of a function are the points where the graph crosses the x-axis or y-axis. These points can be used to help sketch the graph.
• Using symmetry:Some functions are symmetric about the x-axis, y-axis, or both. This symmetry can be used to help sketch the graph.
• Using transformations:Functions can be transformed by shifting, scaling, or reflecting them. These transformations can be used to create new functions from existing functions.

Limits and Continuity

Limits and continuity are fundamental concepts in calculus that provide the foundation for understanding the behavior of functions. Limits describe the behavior of a function as its input approaches a specific value, while continuity measures the smoothness of a function at a particular point.

Together, they provide insights into the nature of functions and their properties.

Limits

A limit describes the value that a function approaches as its input gets closer and closer to a specific value, known as the limit point. It is denoted as:“`lim_(x->a) f(x) = L“`where:* x is the input variable

• a is the limit point
• f(x) is the function
• L is the limit value

There are several methods for evaluating limits, including:*

-*Direct substitution

If f(a) is defined, then lim_(x->a) f(x) = f(a).

• -*Factoring

  If f(x) can be factored into simpler terms, then the limit can be evaluated by factoring out the common factors and simplifying.

-*L’Hopital’s rule

If lim_(x->a) f(x) and lim_(x->a) g(x) are both 0 or both infinity, then lim_(x->a) f(x)/g(x) = lim_(x->a) f'(x)/g'(x), provided that the derivatives exist.

Continuity

A function is said to be continuous at a point a if the following three conditions are met:* f(a) is defined.

• lim_(x->a) f(x) exists.
• lim_(x->a) f(x) = f(a)

Geometrically, a continuous function can be drawn without lifting the pen from the paper. Continuity is important because it ensures that the function can be differentiated and integrated.

Derivatives

The derivative of a function measures the instantaneous rate of change of the function with respect to its input. Geometrically, the derivative at a point is equal to the slope of the tangent line to the graph of the function at that point.

Methods for Finding Derivatives

There are several methods for finding derivatives, including:

• Power Rule:If f(x) = x^n, then f'(x) = nx^(n-1).
• Product Rule:If f(x) = g(x)h(x), then f'(x) = g'(x)h(x) + g(x)h'(x).
• Quotient Rule:If f(x) = g(x)/h(x), then f'(x) = (h(x)g'(x) – g(x)h'(x))/h(x)^2.
• Chain Rule:If f(x) = g(h(x)), then f'(x) = g'(h(x))h'(x).

Applications of Derivatives

Derivatives have numerous applications in calculus, including:

• Finding critical points (points where the derivative is zero or undefined).
• Finding local extrema (points where the derivative changes sign).
• Determining concavity (whether the graph of the function is concave up or concave down).

Applications of Derivatives

Derivatives find widespread applications in various fields, including optimization, related rates problems, and curve sketching. By understanding the rate of change of a function, we can solve complex problems involving extrema, instantaneous rates, and the behavior of functions.

Optimization Problems

Derivatives enable us to find the maximum and minimum values of a function within a given interval. This is crucial in fields like economics, engineering, and manufacturing, where optimizing outcomes is essential. For instance, a company can use derivatives to determine the optimal production level that maximizes profit.

Related Rates Problems

Related rates problems involve finding the rate of change of one variable with respect to another when both variables are changing simultaneously. Derivatives allow us to determine these rates and solve problems in areas like physics, fluid dynamics, and kinematics.

For example, we can use derivatives to calculate the rate at which the volume of a balloon changes as it is being inflated.

Curve Sketching

Derivatives provide valuable information about the shape and behavior of a function’s graph. By analyzing the sign of the derivative, we can identify critical points, intervals of increase/decrease, and concavity. This information is essential for sketching accurate graphs and understanding the function’s characteristics.

Integrals

An integral is a mathematical operation that calculates the area under the curve of a function. Geometrically, the integral of a function represents the net area between the graph of the function and the x-axis over a given interval.

Methods for Finding Integrals, Ap calculus ab first semester review

There are several methods for finding integrals, including:

• Power Rule:Used to integrate polynomials, where the integral of x^n is (x^(n+1))/(n+1) + C.
• Substitution:Used when the integrand can be expressed as a composite function, where u = g(x) and du/dx = g'(x).
• Integration by Parts:Used when the integrand is a product of two functions, where ∫ u dv = uv – ∫ v du.
• Trigonometric Substitution:Used when the integrand involves trigonometric functions, such as sin(x) or cos(x).

Applications of Integrals

Integrals have wide applications in various fields, including:

• Finding Volumes:Used to calculate the volume of solids of revolution, such as cylinders, cones, and spheres.
• Finding Areas:Used to calculate the area of regions bounded by curves, such as finding the area under a normal distribution curve.
• Finding Work:Used to calculate the work done by a force over a distance, such as the work done by a spring.

Applications of Integrals

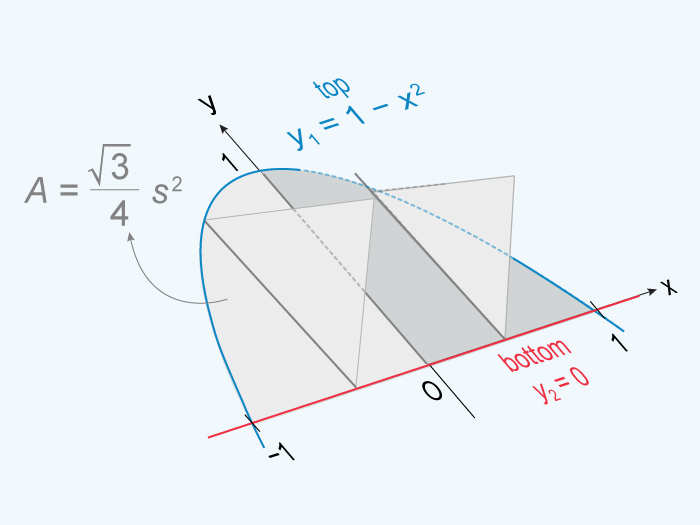
Integrals find numerous applications in various fields, including solving differential equations, calculating the center of mass, and determining moments of inertia.

Solving Differential Equations

Integrals play a crucial role in solving differential equations, which describe the rate of change of a quantity over time. By integrating both sides of a differential equation, we can find the original function that satisfies the equation.

Finding the Center of Mass

The center of mass of a region or an object is the point where the entire mass can be considered concentrated. Integrals can be used to calculate the center of mass by dividing the integral of the mass distribution over the region by the total mass.

Calculating Moments of Inertia

Moments of inertia are quantities that measure the resistance of an object to angular acceleration. Integrals are used to calculate the moments of inertia for various objects, such as rods, disks, and spheres.

Real-World Applications

• Finding the area under a curve to determine the volume of a solid of revolution.
• Calculating the work done by a force over a distance.
• Determining the center of gravity of an object.
• Modeling population growth or decay using differential equations.
• Analyzing the motion of objects in physics.

Questions and Answers

What is the significance of limits in calculus?

Limits play a crucial role in calculus as they provide a precise way to describe the behavior of functions as their inputs approach specific values or infinity. They are essential for defining derivatives, integrals, and other fundamental concepts of calculus.

How can I improve my understanding of derivatives?

Practice is key to mastering derivatives. Engage in solving various types of derivative problems, including those involving the power rule, product rule, quotient rule, and chain rule. Additionally, visualize the geometrical interpretation of derivatives as the slope of the tangent line to a function’s graph.

What are the practical applications of integrals?

Integrals have a wide range of applications in science and engineering, including finding areas and volumes of irregular shapes, calculating work done by forces, and solving differential equations. They are essential tools for modeling and analyzing real-world phenomena.